I/ Mappy.

Nous allons rechercher avec Mappy le plus court chemin pour aller de Rennes à Marseille. Cliquez sur l'image suivante pour vous rendre sur Mappy.

Le chemin le plus rapide permet d'arriver en combien de temps ? Combien aura-t-on parcouru de kilomètres? Combien cela coûtera-t-il en péages ?

Le chemin le plus court permet d'arriver en combien de temps ? Combien aura-t-on parcouru de kilomètres? Combien cela coûtera-t-il en péages ?

II/ Le plus court chemin.

Pour trouver le chemin permettant d'aller de Rennes à Marseille, Mappy a utilisé un algorithme. Voyons un peu comment cela fonctionne en cliquant sur la vidéo suivante (vous constaterez qu'il s'agit d'une image animée reproduisant l'algorithme de Dijktra sur l'exemple de la vidéo.), (faites bien attention, vous allez devoir faire le raisonnement sur le graphe fourni plus bas):

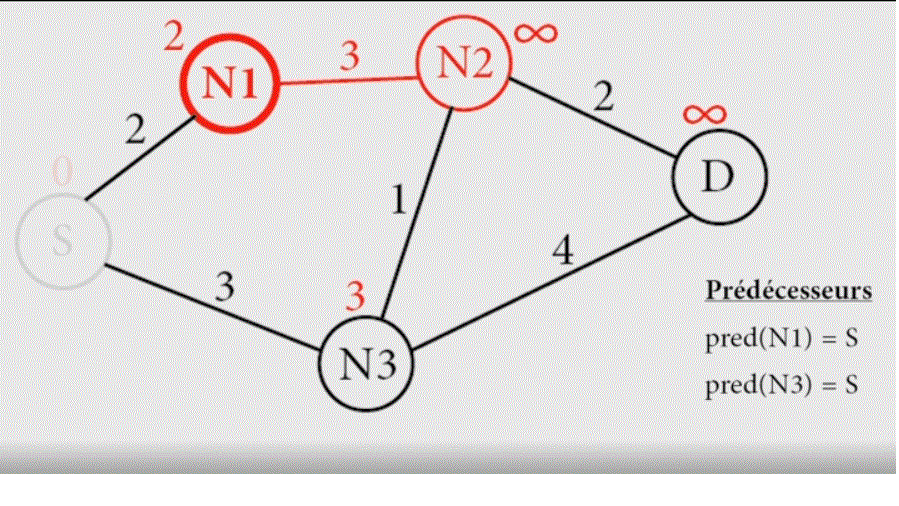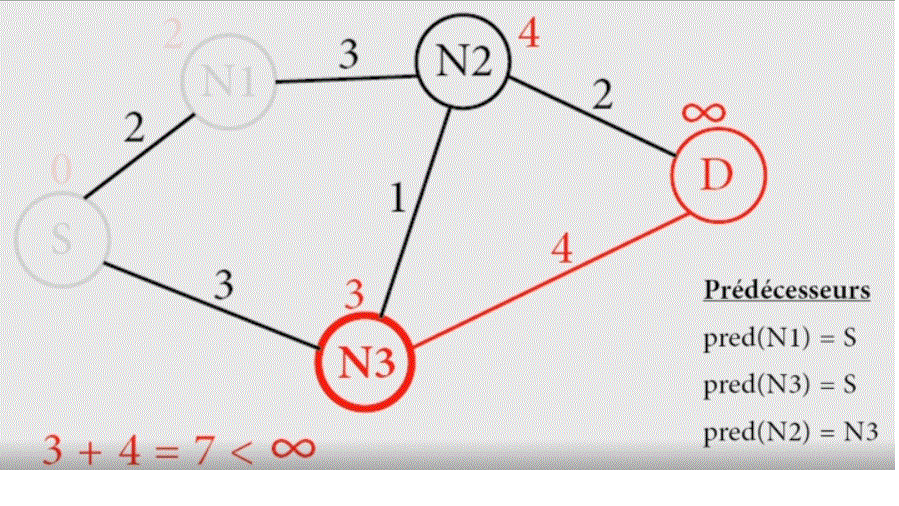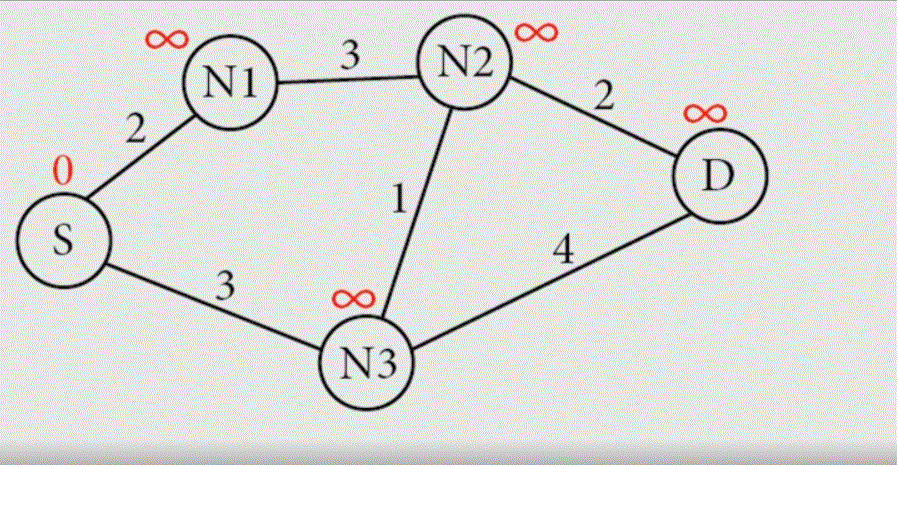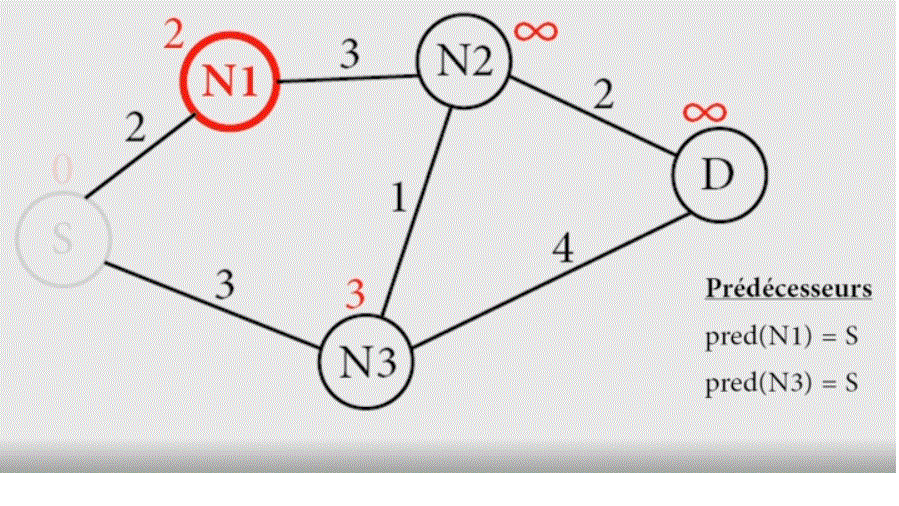
Essayons d'appliquer l'algorithme de Dijstra pour découvrir manuellement le plus court chemin pour aller de Rennes à Marseille. Pour cela, j'ai construit ci-dessous un graphe simplifié représentant les distances entre différentes grandes villes de France.

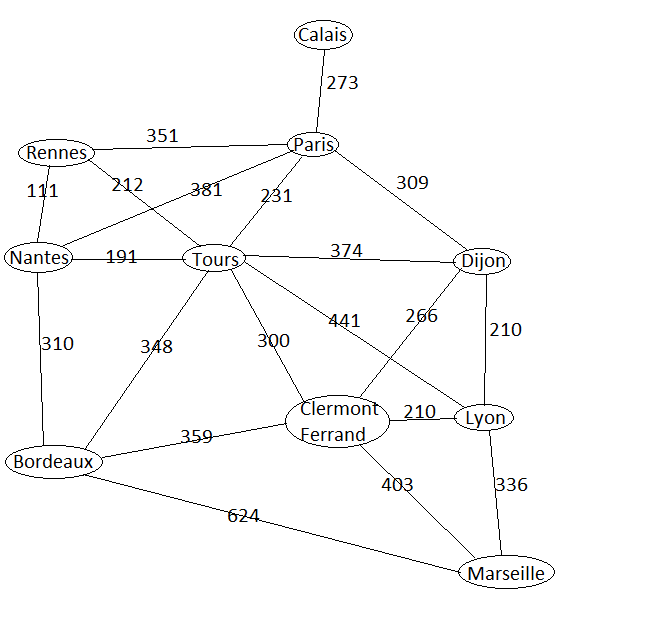
Faisons fonctionner l'algorithme:

• Posez des infinis (nombre très très grand) sur chaque ville et 0 sur Rennes..
• Faîtes tourner la boucle suivante:
1. Prendre le sommet ayant le poids le plus faible.
2. Regarder les sommets adjascents (qui le touchent) et remplacer leur poids par la valeur du sommet précédent + la valeur de l'arrête si cette somme est inférieure à la valeur du sommet. S'il y a remplacement, écrire : préd (........) = .........
3. Puis rayer le sommet.

Pour vérfier votre résultat, ouvrir Spyder, et copier coller le programme suivant.

Pensez à enregistrer votre travail dans:
votre dossier de classe/votre nom/5 carto/TP4.

Appelez le :

Dijkstra

Puis lancez le programme:

graphe_villes={'Calais':{'Paris':273},
    'Rennes':{'Paris':351,'Tours':212,'Nantes':111},
    'Paris':{'Calais':273,'Rennes':351,'Nantes':381,'Tours':231,'Dijon':309},
    'Nantes':{'Rennes':111,'Paris':381,'Tours':191,'Bordeaux':310},
    'Tours':{'Paris':231,'Rennes':212,'Nantes':191,'Bordeaux':348,'Clermont Ferrand':300,'Lyon':441,'Dijon':374},
    'Dijon':{'Paris':309,'Tours':374,'Clermont Ferrand':266,'Lyon':210},
    'Bordeaux':{'Nantes':310,'Tours':348,'Clermont Ferrand':359,'Marseille':624},
    'Clermont Ferrand':{'Bordeaux':359,'Marseille':403,'Lyon':210,'Dijon':266,'Tours':300},
    'Lyon':{'Dijon':210,'Tours':441,'Clermont Ferrand':210,'Marseille':336},
    'Marseille':{'Lyon':336,'Clermont Ferrand':403,'Bordeaux':624}}
 
 
def dijkstra_PCC(G,depart,arrivee,visites=None,distance=None,predecesseur=None):
    visites = visites or []
    distance = distance or {}
    predecesseur = predecesseur or {}
    if depart not in G:
        raise TypeError
    if arrivee not in G:
        raise TypeError
    if depart==arrivee:
        chemin=[]
        pred=arrivee
        while pred!=None:
            chemin.append(pred)
            pred=predecesseur.get(pred,None)
        print('plus court chemin:'+str(chemin)+"distance(km)="+str(distance[arrivee]))
    else:
        if not visites:
            distance[depart]=0
        for voisin in G[depart]:
            if voisin not in visites:
                nouvelle_dist=distance[depart]+G[depart][voisin]
                if nouvelle_dist<distance.get(voisin,float('inf')):
                    distance[voisin]=nouvelle_dist
                    predecesseur[voisin]=depart
        visites.append(depart)
        nonvisites={}
        for i in G:
            if i not in visites:
                nonvisites[i]=distance.get(i,float('inf'))
        x=min(nonvisites, key=nonvisites.get)
        dijkstra_PCC(G,x,arrivee,visites,distance,predecesseur)
 
if __name__ == '__main__':
    dijkstra_PCC(graphe_villes, "Rennes", "Marseille")

Je vous propose de demander à votre programme d'effectuer un autre calcul de plus court chemin. Dans la dernière ligne de votre programme, remplacez Rennes par Calais.

Pensez à enregistrer votre travail dans:
votre dossier de classe/votre nom/5 carto/TP4.

Appelez le :

DijkstraCalais

Puis lancez le pour connaître la plus courte distance entre Calais et Marseille.

Vous constaterez qu'en début de programme, un catalogue a été saisi, indiquant la valeur des arêtes entre les différentes villes qui sont directement liées entre elles. Le graphe a été numérisé.

III/ Revenons sur Open Street Map et Python.

Nous allons demander à un programme Python de nous indiquer toutes les étapes intermédiaires (coordonnées géographiques) pour aller d'un point à un autre. Pour réaliser cela, notre programme python aura besoin de la bibliothèque pyroutelib3 qui utilise les cartes d'Open Street Map.

Ouvrez Syder.

Copier coller le programme ci-dessous

Pensez à enregistrer votre travail dans:
votre dossier de classe/votre nom/5 carto/TP4.

Appelez le :

Itin

Puis lancez le

from pyroutelib3 import Router
router = Router("car")
depart = router.findNode(46.465973, -0.806519)
arrivee = router.findNode(46.483708,  -0.751276)
status, route = router.doRoute(depart, arrivee)
if status == 'success':
    routeLatLons = list(map(router.nodeLatLon, route))

Une fois l'exécution du programme terminé (cela peut prendre quelques minutes), à l'aide de "l'explorateur de variables" de spyder, visionnez le contenu de la variable "routeLatLons". Comme vous pouvez le constater, cette variable contient une liste de couples de valeurs (latitude, longitude). Cette liste contient donc les coordonnées des différents points par lesquels il faut passer pour se rendre du point de départ jusqu'au point d'arrivée (en passant bien évidemment par les routes définies dans Open Street Map).

Quelques explications sur le programme ci-dessus:

Nous commençons par importer la bibliothèque "pyroutelib3" avec la première ligne.

La deuxième ligne permet de définir le véhicule qui sera utilisé pour effectuer le trajet. Il est possible de choisir: cycle, car, foot, horse, tram, train

Les deux lignes suivantes permettent de définir le point de départ et le point d'arrivée à l'aide de leur coordonnées géographiques en DD.

La ligne suivante permet d'effectuer le calcul de l'itinéraire.

La dernière ligne est exécutée uniquement si le calcul est mené à son terme. La variable "routeLatLons" contient la liste des coordonnées des points de cheminement.

Avoir une liste de coordonnées, c'est bien, mais visualiser sur une carte, c'est mieux. Nous allons donc comme dans le TP 3 faire appel à la bibliothèque folium et visualiser sur une carte notre itinéraire.

Pour cela, copier coller le programme suivant à la place du précédent, et enregistrez le.

from pyroutelib3 import Router
import folium

router = Router("car")
depart = router.findNode(46.465973, -0.806519)
arrivee = router.findNode(46.483708,  -0.751276)
status, route = router.doRoute(depart, arrivee)
if status == 'success':
    routeLatLons = list(map(router.nodeLatLon, route))

c= folium.Map(location=[46.475, -0.78],zoom_start=15)
for coord in routeLatLons:
    coord=list(coord)
    folium.Marker(coord).add_to(c)
c.save('maCarte.html')

Comme vous pouvez le constater, nous ajoutons un marqueur pour chaque couple de coordonnées dans une boucle for, et à la fin, nous sauvegardons le tout dans le fichier maCarte.html

Allez dans votre dossier de classe/espace d'échange/SNT/votre nom/5 carto/TP 4 et ouvrez avec Google le fichier maCarte.html

Quelles sont les villes reliées?

Modifiez le programme précédent pour aller de Pissotte à Mervent. Vous irez chercher les coordonnées géographiques de chacune de ces deux villes avec Géoportail par exemple.